Stoichiometry is the study of the chemical ratios that cause chemical reactions to work the way they do. To really understand stoichiometry, let's start by examining how to "balance" a chemical equation. If I was studying a reaction, and I figured out that my reactants were C2H6 and O2, and my products are H2O and C2O, I need to balance this equation. Another way of thinking about this is, "How can I get the same number of atoms of each element on both sides of the equation?" Essentially, I have to realize that this equation produces three water molecules and two carbon dioxide molecules, and requires two oxygen molecules and one ethane molecule. When the molecules are present in this ratio, they complete this reaction without any difficulty.
So what would happen if one of these elements was not sufficient to complete the reaction--for example, if there was only one oxygen molecule instead of two for every ethane molecule? Well, this is what is known as a "limiting reagent" or a "limiting reactant."
To understand this idea a little better, let's do an example problem. (I can't claim credit for this one; I found it here.) If we have two grams of ammonia react with four grams of oxygen, then what will happen? Well, let's start by balancing the equation.
4 NH3 + 5 O2 ----> 4 NO + 6 H2O
Let's examine one of the products and see which reactant is the limiting reactant. A molar-mass conversion gives us
2 g NH3 x (1 mol NH3/17 g NH3) x (4 mol NO/4 mol NH3) x (30 g NO/1 mol NO) = 3.53 g NO
4 g O2 x (1 mol O2/32 g O2) x (4 mol NO/5 mol O2) x (30 g NO/1 mol NO) = 3 g NO
Here, we can see that oxygen is the limiting reagent, because it produces less NO than the 2 g of ammonia by itself would have.
We can also use these techniques to analyze how much of one element is needed to produce a different compound.
For example, let's consider calcium. How much calcium nitrate will be produced from 2 g of calcium?
As always, start with a balanced equation.
3Ca + N2 = Ca3Na2
Then, using molar mass techniques:
2 g Ca x (1 mol Ca/40 g Ca) x (1 mol Ca3N2/3 mol Ca) x (148 g Ca3N2/1 mol Ca3N2)
which gives us about 2.4 g of Ca3Na2.
Finally, these techniques can also be applied to find the percent yield of an equation. Considering the following example, I should expect to get 2.4 g of Ca3Na2 if I mix 2 g of calcium with nitrogen. However, even in a perfectly executed experiment, this won't be the case, for various reasons. If I recieved, say, 2 g of calcium nitrate, then I can say that my percent yield was about 83%, because 2/2.4 is .83333333....
Thursday, March 15, 2012
Moles: Not Something in Holes
A couple of the ideas we've discussed in this class have been the moles and molar ratios. A mole is just a unit of a number of atoms--more precisely, 1 mol (the somewhat pointless abbreviation for mole) is approximately equal to 6.02x10^23 atoms. Having this unit of measurement is nice because it allows us to convert different substances into units that can be solved for. Let's do some molar calculations to see how this can be applied.
Let's try to answer this problem: How many moles are in 37 grams of copper?
This question is easy enough to answer. The molar weight (as given on a periodic table) of copper is about 63.54 (1 mole weighs about 63.54 g). Dividing, this shows us that 37 g is about .58 mols.
Now, let's move on to a more advanced problem. What if I asked how many atoms were in 37 g of copper?
It's probably easiest, at this point, to use a visual aid to find the solution for this problem.
Looking at this, we can see that the units, in essence "cancel out," leaving behind atoms Cu. Solving, we can see that this gives us about 3.49x10^23 atoms.
We'll do several more problems with this technique throughout the course of this blog.
Let's try to answer this problem: How many moles are in 37 grams of copper?
This question is easy enough to answer. The molar weight (as given on a periodic table) of copper is about 63.54 (1 mole weighs about 63.54 g). Dividing, this shows us that 37 g is about .58 mols.
Now, let's move on to a more advanced problem. What if I asked how many atoms were in 37 g of copper?
It's probably easiest, at this point, to use a visual aid to find the solution for this problem.
| 37 g Cu | 1 mol Cu | 6.02x10^23 atoms Cu |
| 63.54 g Cu | 1 mol Cu |
Looking at this, we can see that the units, in essence "cancel out," leaving behind atoms Cu. Solving, we can see that this gives us about 3.49x10^23 atoms.
We'll do several more problems with this technique throughout the course of this blog.
Friday, January 6, 2012
Conductivity Lab
In this lab, we measured the conductivity of various solutions. This was done by mixing compounds with water, and then checking the conductivity with a Vernier conductivity probe (and collecting its data through Logger Pro.
The data provided by the probe show some interesting results. When the conductivity of ionic compounds, such as calcium acetate and sodium acetate, was tested, it was exceptionally high (nearly 3,000 microsiemens per centimeter in the case of sodium acetate). However, when substances that were not ionic in nature, such as molasses or antacid, were tested, they had very little conductivity (in the case of antacid, less than fifty microsiemens per centimeter).
So what do these data mean?
Clearly, there is a trend towards more conductivity in the ionic compounds. What causes this? It's the very nature of the ionic compounds--because there are ions, which have an electrical charge, within the solution, it naturally conducts well. This lab shows that, whenever there is a large disparity between two different results--in this case, the conductivity of ionic and non-ionic compounds--there is a reason for this, and noticing this is one of the primary requirements for a research scientist.
The data provided by the probe show some interesting results. When the conductivity of ionic compounds, such as calcium acetate and sodium acetate, was tested, it was exceptionally high (nearly 3,000 microsiemens per centimeter in the case of sodium acetate). However, when substances that were not ionic in nature, such as molasses or antacid, were tested, they had very little conductivity (in the case of antacid, less than fifty microsiemens per centimeter).
So what do these data mean?
Clearly, there is a trend towards more conductivity in the ionic compounds. What causes this? It's the very nature of the ionic compounds--because there are ions, which have an electrical charge, within the solution, it naturally conducts well. This lab shows that, whenever there is a large disparity between two different results--in this case, the conductivity of ionic and non-ionic compounds--there is a reason for this, and noticing this is one of the primary requirements for a research scientist.
Tuesday, January 3, 2012
Chemical Reactions (And a Few Other Things Besides)
I'm tired of trying to make Blogger and LaTeX work nicely together. At this point, it's just becoming another way for me to procrastinate even more. So, I'm admitting defeat.
There are several different types of chemical reactions that can occur. To begin, let's start by examining the simplest--a synthesis reaction. In a synthesis reaction, multiple reactants are combined into several products. For example, iron (II) sulfide is created when iron and sulfur react.
Iron (II) sulfide is an ionic compound--this is an easy enough distinction because iron is a metal, and sulfur is a nonmetal. So we know that iron has lost two electrons to sulfur, and that the offsetting charges have resulted in a bond between the two ions. We use the (II) when naming iron (II) sulfide to distinguish it from iron (III) sulfide. This distinction is important because iron can lose either two or three electrons. In naming ionic bonds, it is important to note that prefixes are not used with the element names--only with covalent bonds.
When writing a formula for a named ionic bond--say, calcium carbonate--then a simple technique can be applied. Take each individual part of the compound--Ca and CO3, and try to find a ratio of the two ions that has an equal charge. Because a calcium ion has a charge of +2, and carbonate has a charge of -2, the ratio is simply 1:1. Calcium carbonate can be written as CaCO3.
WARNING! WARNING! WARNING! Sudden topic change ahead. Massive confusion of the brain may result.
Another type of chemical reaction (remember that? The original topic?) is a decomposition reaction. This is the inverse of a synthesis reaction, where one reactant is split into two or more different products. For example, consider the electrolysis of water, when a current is passed through water. The formula for this reaction would be: 2H2O --> 2H2 + O2. The hydrogen and oxygen contained within the water molecule become hydrogen gas and oxygen gas.
The third type of chemical reaction is a single replacement reaction. This type of reaction involves two reactants, one being a compound of two elements, the other, a single element. In a single replacement reaction, the single element will take the place of an element from the compound. A complement for the single replacement is the double replacement. A double replacement reaction is similar to a single replacement reaction, except that instead of one reactant being an element, both reactants are compounds, and one element in each compound joins the other compound. A generic example of a double replacement would be: AB + CD --> CB + AD.
Finally, there's a combustion reaction. In a combustion reaction, a fire burns in the presence of oxygen. Combustion reactions tend to be exothermic and to result in carbon dioxide and water. In its most general form, we could write: Fuel + O2 --> CO2 + H2O + heat energy.
Afterword
I suppose I should go ahead and finish this off. When naming a covalent bond from a formula, you don't have to worry about various ions. There's a simple technique you can follow. For example, consider the molecule CO2. C represents carbon, so we know that the first part of the name of this molecule is named carbon. To represent the presence of both oxygen atoms, we use the prefix di-, so this become dioxide. Putting it all together gives us carbon dioxide.
Rules were made to be broken, however, and these rules do not apply when acids are formed. When hydrogen bonds with another atom, excluding, of course, hydrogen itself and oxygen, an acid is formed. To name an acid, use the prefix hydro-, then the name of the second atom, using the suffix -ic. For example, HCl would be written as hydrochloric acid.
Exception to the exception: If the second part of the compound is a polyatomic compound (it has multiple atoms), then do not use the hydro- prefix. Instead, simply keep the name of the polyatomic compound and add the -ic suffix if it ends in -ate, and -ous if it ends in -ite.
WARNING! WARNING! WARNING! Sudden topic change ahead. Massive confusion of the brain may result.
Another type of chemical reaction (remember that? The original topic?) is a decomposition reaction. This is the inverse of a synthesis reaction, where one reactant is split into two or more different products. For example, consider the electrolysis of water, when a current is passed through water. The formula for this reaction would be: 2H2O --> 2H2 + O2. The hydrogen and oxygen contained within the water molecule become hydrogen gas and oxygen gas.
The third type of chemical reaction is a single replacement reaction. This type of reaction involves two reactants, one being a compound of two elements, the other, a single element. In a single replacement reaction, the single element will take the place of an element from the compound. A complement for the single replacement is the double replacement. A double replacement reaction is similar to a single replacement reaction, except that instead of one reactant being an element, both reactants are compounds, and one element in each compound joins the other compound. A generic example of a double replacement would be: AB + CD --> CB + AD.
Finally, there's a combustion reaction. In a combustion reaction, a fire burns in the presence of oxygen. Combustion reactions tend to be exothermic and to result in carbon dioxide and water. In its most general form, we could write: Fuel + O2 --> CO2 + H2O + heat energy.
Afterword
I suppose I should go ahead and finish this off. When naming a covalent bond from a formula, you don't have to worry about various ions. There's a simple technique you can follow. For example, consider the molecule CO2. C represents carbon, so we know that the first part of the name of this molecule is named carbon. To represent the presence of both oxygen atoms, we use the prefix di-, so this become dioxide. Putting it all together gives us carbon dioxide.
Rules were made to be broken, however, and these rules do not apply when acids are formed. When hydrogen bonds with another atom, excluding, of course, hydrogen itself and oxygen, an acid is formed. To name an acid, use the prefix hydro-, then the name of the second atom, using the suffix -ic. For example, HCl would be written as hydrochloric acid.
Exception to the exception: If the second part of the compound is a polyatomic compound (it has multiple atoms), then do not use the hydro- prefix. Instead, simply keep the name of the polyatomic compound and add the -ic suffix if it ends in -ate, and -ous if it ends in -ite.
Saturday, December 17, 2011
Bonding (No, This Is Not Part of the Trebuchet [Inside Joke])
(For some reason, I'm fascinated by the fact that each of the three main types of chemical bonding has three syllables.)
(Made you count.)
The Periodic Table: Why?
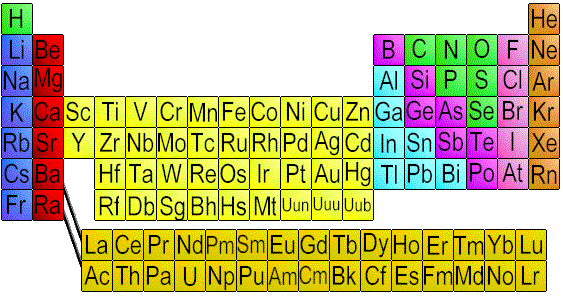
In every chemistry classroom (and I mean every chemistry classroom--I dare you to show me one without this) you'll find something called the periodic table (some editions include "of the elements"). It looks something like this:
At first glance, this seems to be a jumble of random letters. How can all of that have any meaning?
But on deeper investigation, we realize that it's actually quite powerful and organized. It's a tool that is used to group atoms with similar traits together. A basic overview: Going from left to right is a period, and up and down is a group. Across a period, the atomic number increases by increments of one. (Read: Going from left to right--across a period--one atom at a time, atoms gain one proton.) Atoms that are not transition metals (the yellow section in my image above, or groups 3-12--these elements have similar d-block configurations) are in groups with atoms with the same valence electron configuration (valence electrons are the electrons within an atom that are free to form bonds). By definition, this means that atoms in the same group have similar chemical properties, because valence electrons are what define chemical properties.
So, since groups have similar chemical properties...what are those chemical properties?
Well, I'm going to focus on the groups that have been named. Starting from the far left side, we'll find group 1--commonly known as "alkali metals." This group is part of the s-block of the periodic table, meaning that all of its outermost electrons are in the s orbital. Excluding hydrogen (and there is debate over whether or not hydrogen should even be a part of this group) the alkali metals are all extremely reactive metals.
Group 2, commonly known as the "alkaline earth metals," are also in the s-block, and also have all of their outermost electrons in the s orbital. They melt at extremely high temperatures, and are somewhat reactive.
There are other types of element as well, such as the transition metals, the metalloids, and non-metals. Transition metals tend to be mildly reactive, but conduct well because they bond in a way that involves sharing electrons, which in turn allows electrons to flow freely through them. The metalloids have some of the characteristics of metals--for example, both metals and metalloids tend to be solids, but metalloids tend to have a lower density than metals. Non-metals tend to be poor conductors, dull, and britle--each a characteristic unlike those of metals.
On the other end of the table, in group 17, we find the "halogens." As these elements tend to gain electrons, they are also extremely reactive. Once it reacts, however, the resulting molecule tends to be quite non-reactive because of the strength of its reaction. For example, Teflon is made by bonding fluorine with carbon.
And finally, of course, we have the "noble (inert) gases." These are named because of their tendency not to react with other elements. They are all odorless, colorless, non-reactive gases. Noble gases have a full outer shell, which is the reason for their innate inertness.
Sunday, October 16, 2011
The Monster Post
If you're pressed for time and don't want to read the entire post, just read the abstract.
Abstract: When God designed the atom, He had worked a few too many late nights.
Let's go down to the fundamental basics. The basic units of matter are known as elementary particles, such as quarks (which combine in certain combinations to create protons and neutrons) and leptons (such as electrons). We'll take a look at both of these particles.
Quarks come in six flavors: up, down, strange, charm, top and bottom. Each one has a slight distinction that makes it different from the rest, but we'll just focus on the ones that can be found within the nucleus--the up and down quarks. Here's a little table that lists the actual characteristics of each flavor, and then I'll explain what each term means:
| Mass | Spin | Charge | |
| Up | 1.5-3.3 MeV | 1/2 | +2/3 |
| Down | 3.5-6.0 MeV | 1/2 | -1/3 |
(Source: ParticleZoo for iPad)
Although the mass category may seem to be somewhat self-explanatory, it's important to notice that the mass here is measured in mega electron volts. An electron volt is simply a unit of energy (in the quantum world, mass and energy are equivalent, after all--that's why it's called "mass-energy equivalence").
"Spin," however, takes a bit more dedication to wrap our minds around. The "spin" of a quark--or, for that matter, any particle--is a fundamental factor of a particle's quantum state. It was originally thought to be an actual rotation around an axis. This is only correct in that the spin of a particle follows the same mathematical rules as rotation. My understanding of it is that it is a mathematical convenience--a property that needs to be described, but the actual details are not yet clear.
"Charge" is somewhat more intuitive. It simply refers to the attraction or repulsion between different particles. (Although the fact that quarks have fractional charge values is not what we would expect, this can be explained in part by the fact that quarks have never been found without being coupled with other quarks that provide a discrete, integer value.)
The varying charges of up and down quarks provide us with a way of explaining the charges of a proton and a neutron. When two up quarks and one down quark combine (via the strong interaction), the total charge is simply:
$\frac{2}{3}+\frac{2}{3}-\frac{1}{3}=1$
Whearas for a neutron, with one up quark and two down quarks, the charge is:
$\frac{2}{3}-\frac{1}{3}-\frac{1}{3}=0$
Now, protons and neutrons combine to form the nucleus of an atom--that's basic enough. The combined number of protons and neutrons is the mass number--it essentially tells you how heavy the atom is. The reason elements such as lead are so heavy is that they have a relatively high mass number. Atomic mass, on the other hand, is a weighted average of the isotopes of an atom. It isn't a whole number--even though it is an average of whole numbers. The atomic number simply tells you how many protons are in the nucleus of an atom. For example, lead's atomic number is 82, so it has 82 protons in its nucleus.
That's the boring part of an atom. The real fun begins when you start to consider what happens around the nucleus--with these leptons (another type of particle) known as electrons. Electrons, in case you actually care, have a spin of 1/2 and a charge of -1 (big surprise there). However, what we really care about is where those electrons are and how they behave. Unfortunately for us, the best answer we can give is...we don't know. The issue is that we can't figure out where an electron is at any given moment. I read an analogy--I can't remember where--comparing this principle (the Heisenberg uncertainty principle) to an attempt to find a balloon floating around a dark room. The only way to find the balloon is to bump into it--thereby changing its position.
So what can we do to describe the behavior of electrons?
Well, the primary method used is to describe where the electrons are most likely to be at any given point in time. Mathematically, there is no issue with providing, say, a 90% certainty that an electron will be in a certain region at a certain time. Sure, there are equations that can provide these numbers--but I really don't feel like dealing with them in LaTeX right now. If you do, feel free to leave the string in the comments. I'll throw it in and give you credit.
Now, while an electron is flitting around in those regions where it either is or is not supposed to be, it does some pretty bizarre things. One of those involves acting like a wave, even though it's supposed to be a particle. (Even better--all particles act like a wave. That's called "wave-particle duality.") We don't observe larger objects acting like a wave because their mass is so comparatively huge that their wavelength is incredibly tiny. Why does the mass matter? Well, that's given by another equation:
$\lambda=\frac{h}{mv}$
This equation essentially assigns a wavelength to particles. It suggests that the wavelength of anything is equal to h (the Planck constant--the smallest possible unit of energy, a.k.a. "quanta") divided by the momentum that object has. Objects with a large amount of mass when compared to an electron have a large amount of momentum compared to the Planck constant, so their wavelength is comparatively tiny.
So, as we add on more and more electrons to the "electron cloud" (it sounds so high-tech), how do they join the group?
To understand this, you have to understand orbitals and energy levels. Let's look at a diagram of the periodic table, conveniently hot-linked to eat up your bandwidth:
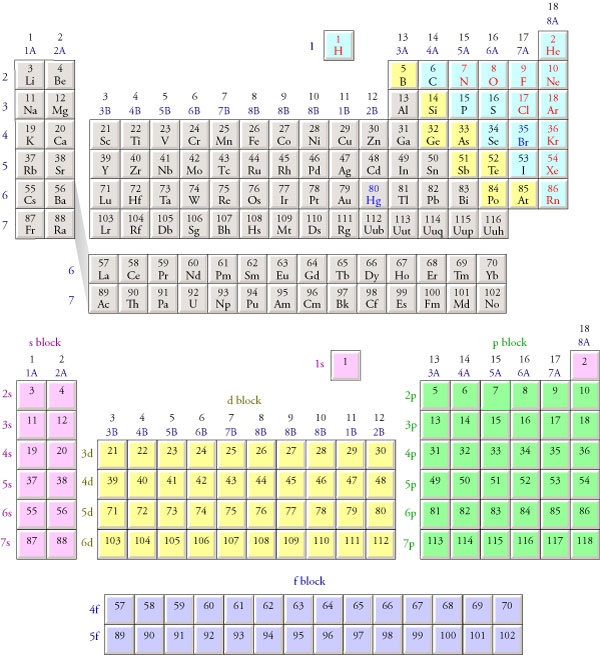
On the lower version, we notice these chunks called "blocks." Those each represent orbitals of energy levels. The purple writing along the left hand side shows, "1s, 2s, 3s..." and so on. This is the "s" orbital, which can hold two electrons--that's why each period has two purple cells. A hydrogen atom has one electron, in the 1s state (the s orbital of the first energy level). Helium will have two electrons, both in the 1s state. (This is commonly denoted as "1s2.") Continuing on to, say, Boron, we notice that it will have, once again, two electrons in 1s, two more in 2s, and another one in 2p. (Each orbital has a different shape, which is how they're distinguished, but I don't feel like going into that, do you?)
So then, the question becomes: How on earth was any of this ever figured out?
Well, once upon a time, the atomic model was a lot simpler. In fact, it was believed that the atom was the fundamental unit of all matter. A lot of this theory was developed and supported by a man named John Dalton. (I got into a little spat last year at Colorado State Knowledge Bowl over what exactly that theory was called, so it shall remain nameless here.)
As time went on, it became clearer that this was not the case. Another scientist named Rutherford discovered the electron by creating a stream of them through a vacuum tube between two plates. Because this stream was repelled by the negative end of a charged plate and attracted by the positive end, it was accepted that these subatomic particles were negatively charged.
Niels Bohr did some work with spectroscopy (analyzing the wavelengths of light emitted by elements) and designed another model. Our chemistry class actually repeated some of these experiments, and although I wasn't capable of taking beautiful pictures, I'll be more than happy to hotlink more in for you:
Bohr thought that electrons were emitting photons only at these specific frequencies because they were confined to certain orbits around the nucleus. Electrons could not be in the middle of two energy levels. When an electron was bumped up an energy level, it made a "quantum leap," causing it to emit a photon. (Incidentally, this kind of a spectrum, where photons are being emitted by the material being examined, is known as an emission spectrum.)
Here's the issue with the Bohr model, however: it's wrong. It doesn't explain the emission spectra of atoms with more than one electron (read: everything but hydrogen), and it gives electrons a definite position--which violates our old friend the Heisenberg Uncertainty Principle.
Well, I think that's all for now. If my abstract didn't make sense before, go back and read it again. It will now. I'm sure I'll be back soon with additions to make this post even longer!
To understand this, you have to understand orbitals and energy levels. Let's look at a diagram of the periodic table, conveniently hot-linked to eat up your bandwidth:

On the lower version, we notice these chunks called "blocks." Those each represent orbitals of energy levels. The purple writing along the left hand side shows, "1s, 2s, 3s..." and so on. This is the "s" orbital, which can hold two electrons--that's why each period has two purple cells. A hydrogen atom has one electron, in the 1s state (the s orbital of the first energy level). Helium will have two electrons, both in the 1s state. (This is commonly denoted as "1s2.") Continuing on to, say, Boron, we notice that it will have, once again, two electrons in 1s, two more in 2s, and another one in 2p. (Each orbital has a different shape, which is how they're distinguished, but I don't feel like going into that, do you?)
So then, the question becomes: How on earth was any of this ever figured out?
Well, once upon a time, the atomic model was a lot simpler. In fact, it was believed that the atom was the fundamental unit of all matter. A lot of this theory was developed and supported by a man named John Dalton. (I got into a little spat last year at Colorado State Knowledge Bowl over what exactly that theory was called, so it shall remain nameless here.)
As time went on, it became clearer that this was not the case. Another scientist named Rutherford discovered the electron by creating a stream of them through a vacuum tube between two plates. Because this stream was repelled by the negative end of a charged plate and attracted by the positive end, it was accepted that these subatomic particles were negatively charged.
Niels Bohr did some work with spectroscopy (analyzing the wavelengths of light emitted by elements) and designed another model. Our chemistry class actually repeated some of these experiments, and although I wasn't capable of taking beautiful pictures, I'll be more than happy to hotlink more in for you:
 |
| Here's hydrogen. |
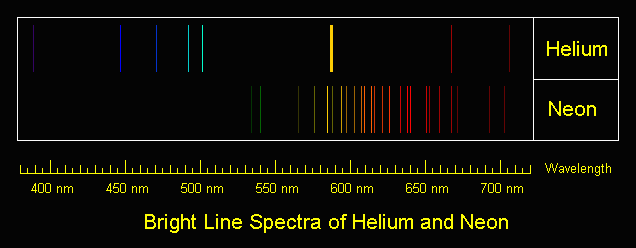 |
| Surprise! It's...helium and neon. |
Here's the issue with the Bohr model, however: it's wrong. It doesn't explain the emission spectra of atoms with more than one electron (read: everything but hydrogen), and it gives electrons a definite position--which violates our old friend the Heisenberg Uncertainty Principle.
Well, I think that's all for now. If my abstract didn't make sense before, go back and read it again. It will now. I'm sure I'll be back soon with additions to make this post even longer!
Subscribe to:
Posts (Atom)